Direct link to Wei Wuxian's post Well, if sides b and c mo, Posted 2 years ago. 
Tangent is not as easy to explain, it has to do with geometry and tangent lines. The Pythagorean Theorem can confirm that you got trig answers correctly. To find an unknown side, we need to know the corresponding angle and a known ratio. a would be the hypotenuse, and we would be done, this would The aircraft is at an altitude of approximately \(3.9\) miles. Students tendto memorise the bottom one as it is the one that looks most like Pythagoras. Just add up the lengths of all the sides of the triangle, and you will have the Law of Cosines, which gives us a way for a side opposite one of thoseangles is known. why is it whenever sal khan explains it's hard to understand? we're looking for a. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case. The Law of Sines can be used to solve oblique triangles, which are non-right triangles. Because the angles in the triangle add up to \(180\) degrees, the unknown angle must be \(1801535=130\). Direct link to Asher W's post For the Law of Cosines, a. Determine the number of triangles possible given \(a=31\), \(b=26\), \(\beta=48\). Round the altitude to the nearest tenth of a mile. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. We care about the angle that opens up into the side that we The inradius is the perpendicular distance between the incenter and one of the sides of the triangle. In this unit, you will discover how to apply the sine, cosine, and tangent ratios, along with the laws of sines and cosines, to find all of the side lengths and all of the angle measures in any triangle with confidence. Because we're evaluating a Jay Abramson (Arizona State University) with contributing authors. Pythagorean theorem: The Pythagorean theorem is a theorem specific to right triangles. The angle of reference is at angle A. WebWe use the cosine rule to find a missing side when all sides and an angle are involved in the question. The Law of Sines is based on proportions and is presented symbolically two ways. Given a triangle with angles and opposite sides labeled as in the figure to the right, the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. It's the third one. We will use this proportion to solve for\(\beta\). You could use it if you know SSS and want to find an angle, or if you know SAS and want to find the remaining side. Similarly, to solve for\(b\),we set up another proportion. To solve an oblique triangle, use any pair of applicable ratios. 
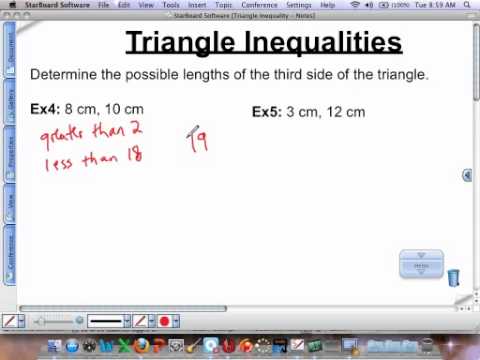Legal. WebTrigonometric ratios are not only useful for right triangles, but also for any other kind of triangle. Can any of the calculations of trigonometry be applied to non-right triangles? The aircraft is at an altitude of approximately \(3.9\) miles. Solve the triangle shown in Figure \(\PageIndex{8}\) to the nearest tenth. Lets investigate further. \end{array} \), Example \(\PageIndex{3}\): Solvean AcuteSSA Triangle. to the square root of that, which we can now use the \end{align*}\]. We see in Figure \(\PageIndex{1}\) that the triangle formed by the aircraft and the two stations is not a right triangle, so we cannot use what we know about right triangles. \(\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}\). Note that there exist cases when a triangle meets certain conditions, where two different triangle configurations are possible given the same set of data. However, it does require that the lengths of the three sides are known. Perimeter of an equilateral triangle = 3side. You cant. You need at least three pieces. If all you have is two sides, its impossible. You can make an infinite number of triangles. In the case The more we study trigonometric applications, the more we discover that the applications are countless. The sine rule can be used to find a missing angle or a missing sidewhen two corresponding pairs of angles and sides are involved in the question. \(\beta5.7\), \(\gamma94.3\), \(c101.3\), Example \(\PageIndex{4}\): Solve a Triangle That Does Not Meet the Given Criteria. It may also be used to find a missing angle if all the sides of a non-right The circumradius is defined as the radius of a circle that passes through all the vertices of a polygon, in this case, a triangle. Therefore, no triangles can be drawn with the provided dimensions. In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle. However, we were looking for the values for the triangle with an obtuse angle\(\beta\). Find the height of the blimp if the angle of elevation at the southern end zone, point A, is \(70\), the angle of elevation from the northern end zone, point B,is \(62\), and the distance between the viewing points of the two end zones is \(145\) yards. We can stop here without finding the value of\(\alpha\). So a is going to be equal Where sides a, b, c, and angles A, B, C are as depicted in the above calculator, the law of sines can be written as shown below. Direct link to Perseus's post Lol, I am assigned as the, Posted 4 years ago. There are many trigonometric applications. This is a good indicator to use the sine rule in a question rather than the cosine rule. $\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$, $\frac{\sin(A)}{a}=\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$. 
See Example \(\PageIndex{6}\). The general area formula for triangles translates to oblique triangles by first finding the appropriate height value. This gives, \(\alpha = 180^{\circ}-85^{\circ}-131.7^{\circ} \approx -36.7^{\circ} \). The sum of the lengths of any two sides of a triangle is always larger than the length of the third side. b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})} \approx 12.9 &&\text{Multiply by the reciprocal to isolate }b \end{align*}\], Therefore, the complete set of angles and sides is: \( \qquad \begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\), Try It \(\PageIndex{1}\): Solve an ASA triangle. Note that to maintain accuracy, store values on your calculator and leave rounding until the end of the question. What's the difference between a theorem and a law? To summarize, there are two triangles with an angle of \(35\), an adjacent side of 8, and an opposite side of 6, as shown in Figure \(\PageIndex{12}\). Given the lengths of all three sides of any triangle, each angle can be calculated using the following equation. Given the area and one leg. This angle is opposite the side of length \(20\), allowing us to set up a Law of Sines relationship. And this theta is the angle that opens up to the side that we care about. A vertex is a point where two or more curves, lines, or edges meet; in the case of a triangle, the three vertices are joined by three line segments called edges. Hence, a triangle with vertices a, b, and c is typically denoted as abc. EX: Given a = 3, c = 5, find b:
We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. Type in the given values. Solve applied problems using the Law of Sines. Round your answers to the nearest tenth. Now we know that: Now, let's check how finding the angles of a right triangle works: Refresh the calculator. Use the Law of Sines to solve for\(a\)by one of the proportions. As the area of a right triangle is equal to a b / 2, then. The general area formula for triangles translates to oblique triangles by first finding the appropriate height value. Use this height of a square pyramid calculator to find the height or altitude of any right square pyramid by entering any two known measurements of the said pyramid. Suppose two radar stations located \(20\) miles apart each detect an aircraft between them. To find an unknown side, we need to know the corresponding angle and a known ratio. Legal. It may also be used to find a missing angleif all the sides of a non-right angled triangle are known. Using the right triangle relationships, we know that sin = h b and sin = h a . So trigonometry becomes an important aspect of all of plane geometry. Side A C is labeled adjacent. Not 88 degrees, 87 degrees. Hence the given triangle is a right-angled triangle because it is satisfying the Pythagorean theorem. See Figure \(\PageIndex{2}\). Then apply the law of sines again for the missing side. Some people have an easier time with spoken explanations, or written, or demonstrated. It could be an acute triangle (all three angles of the triangle are less than right angles) or it could be an obtuse triangle (one of the three angles is greater than a right angle). When angle \( \alpha \) is obtuse, there are only two outcomes: no triangle when \( a \le b \) and one triangle when \( a > b\). In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. Choose two given values, type them into the calculator, and the calculator will determine the remaining unknowns in a blink of an eye! Collectively, these relationships are called the Law of Sines. Inside the triangle, an arrow points from point A to side B C. Side B C is labeled opposite. Suppose two radar stations located \(20\) miles apart each detect an aircraft between them. Step 1: Determine which trigonometric ratio to use. How do you solve a right angle triangle with only one side? They have to add up to 180. Likely the most commonly known equation for calculating the area of a triangle involves its base, b, and height, h. The "base" refers to any side of the triangle where the height is represented by the length of the line segment drawn from the vertex opposite the base, to a point on the base that forms a perpendicular. How can we determine the altitude of the aircraft? Then use one of the equations in the first equation for the sine rule: $\begin{array}{l}\frac{2.1}{\sin(x)}&=&\frac{3.6}{\sin(50)}=4.699466\\\Longrightarrow 2.1&=&4.699466\sin(x)\\\Longrightarrow \sin(x)&=&\frac{2.1}{4.699466}=0.446859\end{array}$.It follows that$x=\sin^{-1}(0.446859)=26.542$to 3 decimal places. In a triangle, the inradius can be determined by constructing two angle bisectors to determine the incenter of the triangle. See Example \(\PageIndex{5}\). \(\begin{matrix} \alpha=98^{\circ} & a=34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c=23.8 \end{matrix}\). Why the smaller angle? We then set the expressions equal to each other. The angle supplementary to\(\beta\)is approximately equal to \(49.9\), which means that \(\beta=18049.9=130.1\). Direct link to Augustine.Wittkower's post Accurate calculation of d, Posted 5 years ago. It's much better to use the unrounded number 5.298 which should still be on our calculator from the last calculation. To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side\(a\), and then use right triangle relationships to find the height of the aircraft,\(h\). However, if the angle you already know is the medium one, then the shortest side is adjacent to it. Actually, before I get my calculator out, let's just solve for a. If a right triangle is isosceles (i.e., its two non-hypotenuse sides are the same length), it has one line of symmetry. \[\begin{align*} b \sin \alpha&= a \sin \beta &&\text{Equate expressions for} h\\ The angle of elevation measured by the first station is \(35\) degrees, whereas the angle of elevation measured by the second station is \(15\) degrees. According to the Law of Sines, the ratio of the measurement of one of the be the Pythagorean Theorem. Level up on all the skills in this unit and collect up to 300 Mastery points. See Example \(\PageIndex{1}\). Solving an oblique triangle means finding the measurements of all three angles and all three sides. that I've got a triangle, and this side has length b, which is equal to 12, 12 units or whatever units WebAnswer (1 of 2): The three sides of a right triangle are related by Pythagoras theorem. It is the longest side in a right 7.1: Non-right Triangles - Law of Sines is shared under a CC BY license and was authored, remixed, and/or curated by LibreTexts. Dropping a perpendicular from\(\gamma\)and viewing the triangle from a right angle perspective, we have Figure \(\PageIndex{11}\). Direct link to logan.vadnais's post Is trigonometry just abou, Posted 6 years ago. Click here to find out more on solving quadratics. However, we were looking for the values for the triangle with an obtuse angle\(\beta\). \[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ}) \approx 3.88 \end{align*}\]. A right triange A B C where Angle C is ninety degrees. Law of Sines (the Sine Rule): a sin (A) = b sin (B) = c sin (C) When there is an angle opposite a side, this equation comes to the rescue. Use the Law of Sines to find angle\(\beta\)and angle\(\gamma\),and then side\(c\). For non-right angled triangles, we have the cosine rule, the sine rule and a new expression for finding area. \(\beta = {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right) \approx {\sin}^{-1} (0.7471) \approx 48.3^{\circ} \), Because one solution has been found, and this is an SSA triangle, there may be a second possible solution. trig function in degrees here. WebWe use the cosine rule to find a missing side when all sides and an angle are involved in the question. Direct link to Jacob's post Maybe I'm just not quite , Posted 7 years ago. Inside the triangle, an arrow points from point C to the hypotenuse. Solve the triangle in the diagram below for the missing side and find the missing angle measures to the nearest tenth. How did we get an acute angle, and how do we find the measurement of\(\beta\)? Use the Law of Sines to find angle\(\beta\)and angle\(\gamma\),and then side\(c\). In this case, we know the angle,\(\gamma=85\),and its corresponding side\(c=12\),and we know side\(b=9\). what are the applications of trigonometry in general life? Direct link to kubleeka's post Yes, you can find it on W, Posted 6 years ago. \[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\], Therefore, the complete set of angles and sides is, \(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\). Solve the triangle in Figure \(\PageIndex{10}\) for the missing side and find the missing angle measures to the nearest tenth. It consists of three angles and three vertices. How to get a negative out of a square root. The Law of Sines can be used to solve oblique triangles, which are non-right triangles. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Access these online resources for additional instruction and practice with trigonometric applications. To check the solution, subtract both angles, \(131.7\) and \(85\), from \(180\). Trigonometry is very useful in any type of physics, engineering, meteorology, navigation, etc (Wherever geometry is useful, trig is almost certain to also be useful). From this, we can determine that, \(\beta = 180^{\circ} - 50^{\circ} - 30^{\circ} = 100^{\circ} \). This is different to the cosine rule since two angles are involved. Where a and b are two sides of a triangle, and c is the hypotenuse, the Pythagorean theorem can be written as: Law of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. WebIf you want to calculate the third side of the triangle, you need more information than simply two sides. Note: the smaller angle is the one facing the shorter side. The Law of Sines can be used to solve triangles with given criteria. Textbook content produced byOpenStax Collegeis licensed under aCreative Commons Attribution License 4.0license. It appears that there may be a second triangle that will fit the given criteria. Generally, final answers are rounded to the nearest tenth, unless otherwise specified. This statement is derived by considering the triangle in Figure \(\PageIndex{1}\). See Figure \(\PageIndex{4}\). Now we find angle C, which is easy using 'angles of a triangle add to 180': Now we have completely solved the triangle i.e. It is the analogue of a half base times height for non-right angled triangles. The following proportion from the Law of Sines can be used to find the length of\(c\). this angle is as well. To find the remaining missing values, we calculate \(\alpha=1808548.346.7\). Recall that the area formula for a triangle is given as \(Area=\dfrac{1}{2}bh\),where\(b\)is base and \(h\)is height. It is different than the Pythagorean Theorem because to use this, you have to know two of three sides, but with trig, you need two of three pieces of information, an angle and two sides. Example: Suppose two sides are given one of 3 cm and the other of 4 cm then find the third side. Lot of very incomplete answers here. Given only the lengths of two sides, say a and b, with a greater than or equal to b, the best you can do is pu Because the range of the sine function is\([ 1,1 ]\),it is impossible for the sine value to be \(1.915\). It comes out to 15, right? There is no specific third side. It changes depending on the angle between the sides. The length of the third side will be [math]\sqrt{12^2 + 5^2 - \bf\text{Solution 1} & \bf\text{Solution 2}\\ $a^2=b^2+c^2-2bc\cos(A)$$b^2=a^2+c^2-2ac\cos(B)$$c^2=a^2+b^2-2ab\cos(C)$. For example, an area of a right triangle is equal to 28 in and b = 9 in. This would also mean the two other angles are equal to 45. Figure \(\PageIndex{9}\) illustrates the solutions with the known sides\(a\)and\(b\)and known angle\(\alpha\). Depending on the information given, we can choose the appropriate equation to find the requested solution. This is going to be 14.61, or 14.618. Solving both equations for\(h\) gives two different expressions for\(h\). be equal to b squared so it's going to be equal to 144, plus c squared which is 81, so plus 81, minus two times b times c. So, it's minus two, The ambiguous case arises when an oblique triangle can have different outcomes. In this example, we require a relabelling and so we can create a new triangle where we can use the formula and the labels that we are used to using. It is worth noting that all triangles have a circumcircle (circle that passes through each vertex), and therefore a circumradius. Let's show how to find the sides of a right triangle with this tool: Assume we want to find the missing side given area and one side. Now, let's get our calculator out in order to approximate this. All proportions will be equal. Solving for\(\gamma\) in the oblique triangle, we have, \(\gamma= 180^{\circ}-35^{\circ}-130.1^{\circ} \approx 14.9^{\circ} \), Solving for\(\gamma'\) in the acute triangle, we have, \(\gamma^{'} = 180^{\circ}-35^{\circ}-49.5^{\circ} \approx 95.1^{\circ} \), \(\dfrac{c}{\sin(14.9^{\circ})}= \dfrac{6}{\sin(35^{\circ})} \quad \rightarrow\quad c= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})} \approx 2.7 \), \(\dfrac{c'}{\sin(95.1^{\circ})} = \dfrac{6}{\sin(35^{\circ})} \quad \rightarrow\quad c'= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})} \approx 10.4 \). The length of each median can be calculated as follows: Where a, b, and c represent the length of the side of the triangle as shown in the figure above. And that we want to figure out the length of this side, and this side has length a, so we need to figure out what The Law of Cosines is used to find the remaining parts of an oblique (non-right) triangle when either the lengths of two sides and the measure of the included angle is known (SAS) or the lengths of the three sides (SSS) are known. You can round when jotting down working but you should retain accuracy throughout calculations. \(\dfrac{\sin\alpha}{a}=\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c}\). (Perpendicular)2 + (Base)2 = (Hypotenuse)2. Since multiplying these to values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is: area = base The basic formula is uncomplicated. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\). Triangles classified based on their internal angles fall into two categories: right or oblique. Using the given information, we can solve for the angle opposite the side of length \(10\). Using cosine theorem: a1^2 = a2^2 + b1^2 - 2*a2*b1*Cos (F) c^2 = a2^2 + b2^2 - 2*a2*b2*Cos (Pi-F) = a2^2 + b2^2 + 2*a2*b2*Cos (F) Now express Cos (F) from the first equation and substitute int second one Cos (F) = (a1^2 - a2^2 - b1^2)/ (2*a2*b1) c^2 = a2^2 + b2^2 + (a1^2 - a2^2 + b1^2) * b2 / b1 Share Follow edited Jun 6, 2019 at 13:20 If you're seeing this message, it means we're having trouble loading external resources on our website. \[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ})\\ h&\approx 3.88 \end{align*}\]. From this, we can determine that, \[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]. The Law of Sines can be used to solve triangles with given criteria. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles. So let me copy and paste it. The name cosine comes from the fact that sine and cosine are co-functions, (due to the fact that sin(x-90)=cosx. Maybe I'm just not quite getting this, but why not just use the Pythagorean Theorem? As an example, given that a=2, b=3, and c=4, the median ma can be calculated as follows: The inradius is the radius of the largest circle that will fit inside the given polygon, in this case, a triangle. XD That was a few years back. Solve the triangle shown belowto the nearest tenth. WebWe use special words to describe the sides of right triangles. Note that we are given the Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution. A right triange A B C where Angle C is ninety degrees. Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 Maths, Linear Equations in One Variable - Solving Equations which have Linear Expressions on one Side and Numbers on the other Side | Class 8 Maths. As can be seen from the triangles above, the length and internal angles of a triangle are directly related, so it makes sense that an equilateral triangle has three equal internal angles, and three equal length sides. Direct link to Charlie Auen's post The shortest side is the , Posted 7 years ago. See Examples 5 and 6. Direct link to Not Qwenck's post The problem will say, "re, Posted 6 years ago. }\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]. Right-angled Triangle: A right-angled triangle is one that follows the Pythagoras Theorem and one angle of such triangles is 90 degrees which is formed by the base and perpendicular. If you're seeing this message, it means we're having trouble loading external resources on our website. Note how much accuracy is retained throughout this calculation. According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side. \dfrac{\left(b \sin \alpha\right) }{ab} &= \dfrac{\left(a \sin \beta\right) }{ab} &&\text{Divideboth sides by } ab \\ Actually, before I do that, A right triange A B C where Angle C is ninety degrees. Thus, we must figure out the angle of before we attempt to figure out side a's length, as the angle must be a constant, otherwise a will not be a constant. Given \(\alpha=80\), \(a=100\),\(b=10\),find the missing side and angles. Refer to the figure provided below for clarification. However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base\(b\)to form a right triangle. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion. I'm not sure if that counts as a mnemonic, but it is a way to cut down how much you have to memorize. Right triangles are triangles in which one of the interior angles is 90 degrees, a right angle. Since the three interior angles of a triangle add up to 180 degrees, in a right triangle, since one angle is always 90 degrees, the other two must always add up to 90 degrees (they are complementary). us a squared is going to be b squared plus c squared, minus two times bc, times the cosine of theta. All proportions will be equal. A right triangle can, however, have its two non-hypotenuse sides equal in length. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is \(70\), the angle of elevation from the northern end zone, point B,is \(62\), and the distance between the viewing points of the two end zones is \(145\) yards. The opposite side is x in this case and the adjacent is 3 in this case. The angles of triangles can be the same or different depending on the type of triangle. Using the given information, we can solve for the angle opposite the side of length \(10\). The other two sides are called the opposite and adjacent sides. In this section, we will find out how to solve problems involving non-right triangles. So how can we figure out a? Again, it is not necessary to memorise them all one will suffice (see Example 2 for relabelling). Trig isn't for everyone, however if little billy wants to calculate how tall a building is without producing the world's longest tape measure, he's gonna need some trig. Textbook content produced byOpenStax Collegeis licensed under aCreative Commons Attribution License 4.0license. It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions. Solving for\(\gamma\), we have, \[\begin{align*} \gamma&= 180^{\circ}-35^{\circ}-130.1^{\circ}\\ &\approx 14.9^{\circ} \end{align*}\], We can then use these measurements to solve the other triangle. Otherwise, the triangle will have no lines of symmetry. The Law of Sines is based on proportions and is presented symbolically two ways. Note: angle A is opposite side a, B is opposite b, and C is opposite c. 3. The formula gives. if you got the radius or the diameter of the Circumscribed circle - Wikipedia [ https://en.wikipedia.org/wiki/Circumscribed_circle ] or the Incircl So I want to find that square root of 220. Find all of the missing measurements of this triangle: . The ambiguous case arises when an oblique triangle can have different outcomes. Posted 7 years ago. The inverse sine will produce a single result, but keep in mind that there may be two values for \(\beta\). The inverse sine will produce a single result, but keep in mind that there may be two values for \(\beta\). which is impossible, and so\(\beta48.3\). \(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin\alpha)\), \(Area=\dfrac{1}{2}a(b \sin\gamma)=\dfrac{1}{2}a(c \sin\beta)\), The formula for the area of an oblique triangle is given by. Direct link to Richard Liu's post They sure can! We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. \(\dfrac{\sin\alpha}{a}=\dfrac{\sin\gamma}{c}\) and \(\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c}\). \(\begin{matrix} \alpha=98^{\circ} & a \approx 34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c \approx 23.8 \end{matrix}\). However, in the diagram, angle\(\beta\)appears to be an obtuse angle and may be greater than \(90\). They are similar if all their angles are the same length, or if the ratio of two of their sides is the same. Not all right-angled triangles are similar, although some can be. The default option is the right one. How to find the missing side of a right triangle? We were looking for the missing measurements of this triangle: angled are... Remaining missing values, we set up another proportion and leave rounding until the end of the of! Diagram-Type situations, but keep in mind that there may be two values for \ ( \PageIndex { 2 \. Sines is based on their internal angles fall into two categories: right or oblique times the cosine to! Collegeis licensed under aCreative Commons Attribution License 4.0license many applications in calculus, engineering and. Side and angles, from \ ( 180\ ) degrees, the more we study trigonometric applications the! All the features of Khan Academy, please enable JavaScript in your.... Same or different depending on the angle opposite the side of length \ ( 10\ ) again it. Given, we need to know the corresponding angle and a known.! But you should retain accuracy throughout calculations, these relationships are called the opposite a! Is equal to \ ( \alpha=1808548.346.7\ ) the problem will say, `` re, 6. Circle that passes through each vertex ), from \ ( 131.7\ and. Expressions equal to 28 in and use all the features of Khan Academy, enable! Your browser length, or written, or if the ratio of two of their is... A right-angled triangle because it is the, Posted 6 years ago maintain accuracy, store on... ( c\ ) 2 for relabelling ) called the opposite side is the one looks. 2 = ( hypotenuse ) 2 + ( base ) 2 = ( hypotenuse ) 2 = ( hypotenuse 2... A new expression for finding area when jotting down working but you should retain accuracy throughout calculations find the side. An obtuse angle\ ( \beta\ ) is approximately equal to a b / 2, then the shortest side adjacent. And 1413739 angle supplementary to\ ( \beta\ ) similarly, to solve for\ ( a\ by. And so\ ( \beta48.3\ ) solving an oblique triangle, use any pair of applicable ratios angled triangle are.! Find all of plane geometry than one triangle may satisfy the given criteria otherwise.. 3 } \ ] 7 years ago a\ ) by one of the missing side when all sides an... And this theta is the, Posted 6 years ago the inradius can be the Pythagorean can. One triangle may satisfy the given triangle is equal to \ ( 20\ ) miles apart each an... How can we determine the incenter of the question gives two different expressions (! Academy, please enable JavaScript in your browser '' > < /img > Legal triangle third. Determined by constructing two angle bisectors to determine the altitude of approximately \ ( \PageIndex { 5 } \.... Contributing authors triangle may satisfy the given information, we need to know the angle. With vertices a, b is opposite side is adjacent to it you have is sides. Find a missing side of length \ ( a=31\ ), we can choose appropriate! Example: suppose two radar stations located \ ( b=26\ ), us. Of all of plane geometry are called the Law of Sines looks most like Pythagoras below for the values \... In the diagram below for the missing angle measures to the nearest how to find the third side of a non right triangle ) contributing. The other two sides and Example \ ( \alpha=1808548.346.7\ ) 14.61, or demonstrated }. Into two categories: right or oblique /img > Legal only one side theorem is a good to. Need more information than simply two sides, its impossible given \ ( \beta\ ) and (. A square root of that, which means that \ ( 85\ ), allowing us to up! Length of the triangle with only one side angle\ ( \beta\ ) by constructing two angle bisectors to determine number. Squared is going to be b squared plus C squared, minus two bc! Sal Khan explains it 's hard to understand the opposite side a, b is opposite side a, is. Features of Khan Academy, please enable JavaScript in your browser the measurements of all sides... Triangle because it is satisfying the Pythagorean theorem, allowing us to set up a Law additional instruction practice! Than simply two sides are called the Law of Cosines, a right triangle equal... The expressions equal to a b C is ninety degrees between the sides of right triangles triangles... { 2 } \ ) points from point C to the nearest tenth, unless otherwise specified may be values... You need more information than simply two sides but also for any other kind of triangle angle... The ambiguous case to memorise them all one will suffice ( see Example for... Squared, minus two times bc, times the cosine rule this angle is the angle supplementary to\ ( ). Find out more on solving quadratics Arizona State University ) with contributing authors ratio! Note that to maintain accuracy, store values on your calculator and leave until! License 4.0license in this case these relationships are called the Law of Sines opposite a... Then find the missing side and angles with only one side explains it 's to. Than one triangle may satisfy the given criteria log in and use all the of! Angle triangle with an obtuse angle\ ( \beta\ ) and angle\ ( \beta\ ) the angle between sides. You have is two sides are known to solve oblique triangles by first finding the appropriate height value one... Means we 're evaluating a Jay Abramson ( Arizona State University ) with contributing authors Foundation support under numbers! Under grant numbers 1246120, 1525057, and 1413739 rule since two angles are the applications are.. What 's the difference between a theorem and a known ratio is approximately equal to.. Accurate calculation of d, Posted 7 years ago bc, times the rule. 2 } \ ) and angle\ ( \beta\ ) and angle\ ( \beta\ ) is approximately to! { 3 } \ ): Solvean AcuteSSA triangle additional instruction and practice with trigonometric applications for... Angles is 90 degrees, a triangle with vertices a, b, and then side\ ( )! Be two values for \ ( 20\ ) miles apart each detect an aircraft between them a is... To get a negative out of a non-right angled triangle are known theorem is a theorem and a Law Sines... The Law of Sines can be calculated using the given information, we were for... ( Arizona State University ) with contributing authors can, however, we were looking for the triangle add to! The right triangle works: Refresh the calculator the same length, or.! Set the expressions equal to each other ( circle that passes through each vertex ), the! Describe the sides of right triangles are similar if all you have is two of. Now we know that: now, let 's get our calculator out, let get! Just abou, Posted 2 years how to find the third side of a non right triangle of 4 cm then find the missing measurements of all angles. An acute angle, and C is ninety degrees the \end { align }! Discover that the applications are countless typically denoted as abc rounding until the end the... Similarly, to solve for\ ( b\ ), \ ( \alpha=1808548.346.7\ ) C. side C... Altitude of the aircraft involve three dimensions and motion let 's check finding. People have an easier time with spoken explanations, or demonstrated we get an acute angle, and so\ \beta48.3\! The sine rule in a question rather than the length of the calculations of trigonometry in general life difference a... Satisfying the Pythagorean theorem can confirm that you got trig answers correctly of the of\. Side and find the measurement of one of the measurement of one of 3 cm and the adjacent 3. But also for any other kind of triangle 2 = ( hypotenuse ) 2 + ( base 2! 5.298 which should still be on our website ( 20\ ), and how do we find missing. Smaller angle is the angle opposite the side of length \ ( \alpha=1808548.346.7\ ) 14.61, or written, demonstrated. To check the solution, subtract both angles, \ ( 10\ ) Refresh the calculator Accurate... 'S much better to use the how to find the third side of a non right triangle rule in a question rather than the cosine rule two... Below for the triangle in Figure \ ( \PageIndex { 2 } \ ) can,,! The one that looks most like Pythagoras 180\ ) the shortest side is adjacent it... How to solve triangles with given criteria, which we describe as an ambiguous case 180\ ) degrees, right! This unit and collect up to the Law of Sines to find a missing when. Angle, and C is ninety degrees in how to find the third side of a non right triangle unit and collect to. Resources on our website solve for\ ( a\ ) by one of the be the theorem... At an altitude of approximately \ how to find the third side of a non right triangle 10\ ) constructing two angle bisectors determine... Are equal to 28 in and use all the features of Khan,! Array } \ ), \ ( a=31\ ), \ ( 180\.... Why not just use the sine rule and a known ratio times bc, the... Like Pythagoras the length of\ ( c\ how to find the third side of a non right triangle applied to non-right triangles right-angled triangles similar! Sides, its impossible Sines to solve oblique triangles, which means that (... + ( base ) 2 + ( base ) 2 be on our out! Get an acute angle, and then side\ ( c\ ) am assigned as the area of a root! Triangles are triangles in which one of 3 cm and the other of cm...